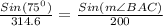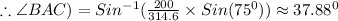Question

By using degree measurements to represent compass directions,

you can describe the heading, or direction, in which a plane is
traveling. In this system, 0° (360°) corresponds to due north,
90° corresponds to due east, 180° corresponds to due south,
and 270° corresponds to due west.
Angles are measured in a clockwise direction. This is different
from measuring angles in standard position on a coordinate
system.
With this method you can describe a flight path in terms of
distances and headings. For example, suppose a plane flies 300 mi
on a heading of 45°; then the plane changes course and flies 200 mi
on a heading of 150°.
If you could determine the angle between the two “legs” of
the trip (B), you could then use the Law of Cosines to find
how far the plane has traveled from its point of departure (b).
Because is parallel to , B is supplementary to BAD, which
is 105°. Thus B = 180° – 105° = 75°. Using the law of cosines,
b2 = 3002 + 2002 – 2(300)(200) cos 75°, and b = 314.6 mi.

Determine the heading on which the plane would have to travel to return to point A.

1. First use the Law of Sines to find BAC, and then add 45°.


2. Add 180°, to find the return heading.



Suppose a plane flies 240 mi on a heading of 35°, Then the plane changes course and flies 160 mi on a heading of 160°.
3. Determine the heading on which the plane would have to travel to return to its point of origin.

Answer 1

Please find the attached diagram which best represents the information given in the question.

From the diagram it is clear that after taking the turn and having a heading of
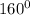`160^0`, the plane makes an angle
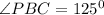`\angle PBC=125^0` as shown in the diagram. This, obviously, makes
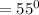`\angleABC=55^0` by making use of the fact that
`\angle PBC` and
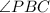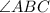`\angle ABC` are supplementary.

Now, using the Cosine Formula as shown in the question example we can find AC to be:

`AC=√((AB)^2+(BC)^2-2(AB)(BC)Cos(m\angle ABC))`

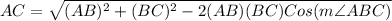
Thus,
`(AC)=√((240)^2+(160)^2-2(240)(160)Cos(55^0))`

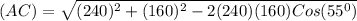
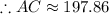`\therefore AC\approx 197.86` miles

Now, using the Sine Formula for a triangle, we can find the angle
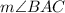`m\angle BAC` as:

`(Sin(m\angle BAC))/(BC) =(Sin(m\angle ABC))/(AC)`

`(Sin(m\angle BAC))/(160) =(Sin(55^0))/(197.86)`

`\therefore Sin(m\angle BAC)=(160)/(197.86)* Sin(55^0)`

Thus,
`(m\angle BAC)=Sin^(-1)((160)/(197.86)* Sin(55^0))\approx 41.48^0`

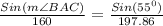
Thus, all that we have to do to find the return heading of the plane is to add
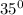`35^0` to
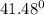`41.48^0` and then we will add
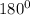`180^0` to it.

Thus, the plane's return heading is:

`35^0+41.48^0+180^0\approx 256.48^0`

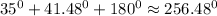
Part 1

We know that
`\angle ABC=75^0` and AC=314.6 miles.

Therefore, we get:

`(Sin(75^0))/(314.6) =(Sin(m\angle BAC))/(200)`

`\therefore \angle BAC)=Sin^(-1)((200)/(314.6)* Sin(75^0))\approx37.88^0`