Answer:
Ration between the volumes = 64:729
Explanation:
If two pyramids are similar and ratio between the lengths of their edges is 4:9
Then we have to tell the ration between their volumes.
Since volume of pyramid
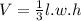
Let length and width of pyramid one are l and w.
So volume of one pyramid
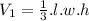
Now by the ratio of 4:9, edges of the second pyramid will be
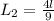

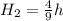
Therefore volume of second pyramid

Now ratio of volumes of both the pyramids =
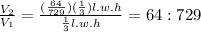
Answer is 64:729 will be the ratio of their volumes.