Answer:
CD and EF
Explanation:
The slope of AB = -4
Two lines are said to be parallel if they have same slopes.
Slope =
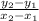
Option 1)J= (8,2) and K (12,3)
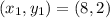
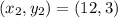
Slope =
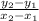
Substitute the values
Slope =
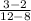
Slope =

Since the Slope of AB and JK is not equal . So, AB and JK are not parallel.
Option 2)C= (6,2) and D (4,10)
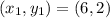
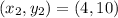
Slope =
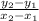
Substitute the values
Slope =

Slope =
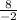
Slope =
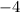
Since the Slope of AB and CD is equal. So, CD is parallel to AB.
Option 3)E= (1,9) and F (2,5)
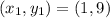

Slope =
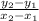
Substitute the values
Slope =
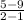
Slope =
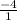
Slope =
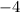
Since the Slope of EF and CD is equal. So, EF is parallel to AB.
Option 4)G= (1,0) and H (1,4)
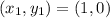
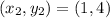
Slope =
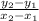
Substitute the values
Slope =
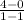
Slope =

Slope =
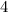
Since the Slope of GH and CD is not equal. So, GH is not parallel to AB.
The slope of AB is equal to the slopes of CD and EF
Hence CD and EF are parallel to AB