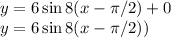Question

What is the general equation of a sine function with an amplitude of 6, a period of pi/4, and a horizontal shift of pi/2?

A.) y=sin (8(x-pi/2))
B.) 8sin(4(x-pi/2))
C.) 6sin (8(x-pi/2)
D,) 6sin(8x)+pi/2

Answer 1

yeah C.

Explanation:

Answer 2

The general equation of the sine function y=f(x) is defined as

`Y=AsinB(x-C)+D`

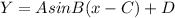
where A is the Amplitude

B represents the frequency of the function with period equals
`2\pi/B`

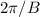
C represents the Horizontal shift, For Phase shift= -C/B

D represents the Vertical shift.

The data given that the amplitude of the function A=6

`B=(2\pi)/(Current\, period)=(2\pi)/(\pi/4)=8`

Vertical shift
`D= 0`

Horizontal Shift
`C= \pi/2`

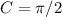
Now plug in
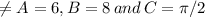`\\eq A=6, B=8\, and \, C=\pi/2` in the general equation of sine function, we get

`y=6\sin8(x-\pi/2)+0\\y=6\sin 8(x-\pi/2))`