The following figure is made of six semicircles with the same diameter, and of four congruent equilateral triangles represented by AEG, EGF, BEF, and GFC. If AE = 3cm, then the area of this figure is, in cm2, equal to:
A)

B)

C)
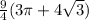
D)

Answer: "C."
Why is it letter "C"?
No matter what I try, I cannot obtain this result. Does anyone know the correct procedure for this?