We will call N the first consecutive positive integer.
Then
N(N + 1) = N + (N +1) +11
N² +N = N + N +1 +11 = N² +N = 2N +12
N² + N - 2N -12 = 0
N² - N - 12 = 0
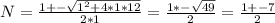
We only need positive integers, then
then N = (1 + 7)/2 = 8/2 = 4
and N + 1 = 4 + 1 = 5
ANSWER two positive consecutive integers are 4 and 5
checking
4*5 = 4+5 +11
20 = 9 +11 = 20 match!!