Question

Consider the error in using the approximation e−x≈1−x on the interval [−1,1]. (a) reasoning informally, on what interval is this approximation an overestimate? 1 an underestimate? (for each, give your answer as an interval or list of intervals,

e.g., to specify the intervals −0.25≤x<0.5 and 0.75

Answer 1

`e^(-x) \approx 1 - x`

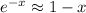
is a classic approximation, true for small x.

The next term in the polynomial expansion will be
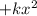`+kx^2` where k is a positive number. So our estimate 1-x is definitely an underestimate on both sides of x=0.

Since for negative xs the exponential rises exponentially and the line only linearly, the exponential exceeds the line for all negative x. For positive x, the line quickly goes negative while the exponential is always positive.

So, there's no interval for which our approximation is an overestimate.