Question

The mean amount spent by a family of four on food per month is $500 with a standard deviation of $75. assuming a normal distribution, what is the probability that a family spends more than $410 per month?

a. 0.1151
b. 0.1539
c. 0.8849.
d. 0.8869
e. none of the above

Answer 1

Let X be the amount spent by a family of four on food per month.

The mean amount spent per month on food is μ = 500

The standard deviation σ =75

X follows Normal distribution with mean μ = 500 and standard deviation σ =75.

The probability that a family spends more than $410 per month is

P(x > 410) =
`P((x-mean)/(standard deviation) > (410 -500)/(75) )`

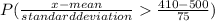
= P(z > -1.2)

= 1 - P(z < -1.2)

Using z score to find probability below -1.2

= 1 - 0.1151

P(x > 410) = 0.8849

The probability that a family spends more than $410 per month is 0.8849