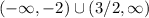Question

For what values of $x$ is $$\frac{x^2 + x + 3}{2x^2 + x - 6} \ge 0?$$ note: be thorough and explain why all points in your answer are solutions and why all points outside your answer are not solutions.

Answer 1

Answer:
`(-\infty, -2)\cup(3/2,\infty)`

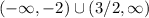
Explanation:

Here, the given expression,

`(x^2 + x + 3)/(2x^2 + x - 6) \geq 0`

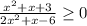
Since, for the value of x,

Denominator ≠ 0,

`2x^2+x-6\\eq 0`

`\implies 2x^2+4x - 3x - 6\\eq =0`

`\implies 2x(x+2)-3(x+2)\\eq 0`

`\implies (2x-3)(x+2)\\eq 0`

`\text{ if }2x-3\\eq 0\implies x\\eq (3)/(2)`

`\text{If } x+2\\eq 0\implies x\\eq -2`

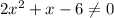
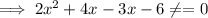
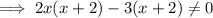
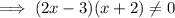
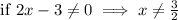
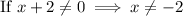
Thus, there is three intervals possible,

1)
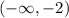
`(-\infty,-2)`

2)
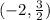
`(-2,(3)/(2))`

3)
`((3)/(2),\infty)`

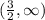
In first intervals,
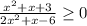`(x^2 + x + 3)/(2x^2 + x - 6) \geq 0` is true.

⇒
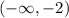`(-\infty,-2)` will contain the value of x.

In second interval,
`(x^2 + x + 3)/(2x^2 + x - 6) \geq 0`

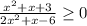
is not true,

⇒
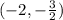`(-2, -(3)/(2))` will not contain the value of x,

In third interval,

In third interval,
`(x^2 + x + 3)/(2x^2 + x - 6) \geq 0`

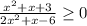
is true,

⇒
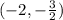`(-2, -(3)/(2))` will contain the value of x,

In third interval,

Thus, the value of x is,

`(-\infty, -2)\cup(3/2,\infty)`

Answer 2

To solve the inequality
`(x^2+x+3)/(2x^2+x-6)\ge \:0`

`\mathrm{Factor\:the\:left\:hand\:side\:}(x^2+x+3)/(2x^2+x-6):`

The numerator
`x^2+x+3` is not factorizable.

so factor the denominator
`2x^2+x-6`:

`2x^2+x-6=\left(2x^2-3x\right)+\left(4x-6\right)=x\left(2x-3\right)+2\left(2x-3\right)\\ \mathrm{Factor\:out\:}x\mathrm{\:from\:}2x^2-3x\mathrm{:\quad }x\left(2x-3\right)\\ \mathrm{Factor\:out\:}2\mathrm{\:from\:}4x-6\mathrm{:\quad }2\left(2x-3\right)\\`

Now take
`\mathrm{Factor\:out\:common\:term\:}\left(2x-3\right)`

Then we get factor of the denominator as
`\left(2x-3\right)\left(x+2\right)`

Thus
`(x^2+x+3)/(2x^2+x-6)=(x^2+x+3)/(\left(x+2\right)\left(2x-3\right))`

Now
`image`

Signs of
`x^2+x+3>0`

`\mathrm{Choosing\:ranges\:that\:satisfy\:the\:required\:condition:}\:\ge \:\:0`

`x<-2\quad \mathrm{or}\quad \:x>(3)/(2)` is the required solution of the given inequality.