Question

1[s] = km for a simple enzymatic reaction. when substrate concentration is tripled, the rate becomes _____ vmax.

Answer 1

The problem can be solved with the help of Michaelis Menten kinetics.

The equation can be written as

`V_(o)= (V_(max)[S])/(K_(m)+ [S])`

Where Vo = Initial velocity of the enzyme. This is also known as initial rate of the reaction.

Vmax = Maximum velocity

[S] = Substrate concentration

Km = Michaelis constant for the given enzyme.

When the substrate concentration is tripled, [S] becomes 3[S]

Let us plug this in Michaelis equation.

The new equation that we get is,

`V_(o)= (V_(max)* 3[S])/(K_(m)+ 3[S])`

We have been given that Km = [S]

Let us write [S] in place of Km in our equation. We get,

`V_(o)= (V_(max)* 3[S])/([S]+ 3[S])`

On adding the values on the denominator we get,

`V_(o)= (V_(max)* 3[S])/(4[S])`

We can cancel out [S] .

`V_(o)= (V_(max)* 3)/(4)`

`V_(o)= (3)/(4)V_(max)`

`V_(o)= 0.75 V_(max)`

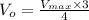
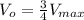
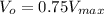
From the above equation, we can see that initial rate of the reaction (V₀) becomes 0.75 times Vmax

Therefore, when substrate concentration is tripled, the rate becomes 0.75 Vmax