Question

Factor, if possible. If the polynomial is prime, say so

w2 + 8w + 16
Factor completely. If the polynomial is prime, say so
35x2 - 2x - 1
Factor using the AC method. If the polynomial is prime, say so.
3y2 + 10y + 7

For the first two problems, factor the polynomials using whatever strategy seems appropriate. State what methods you will use and then demonstrate the methods on your problems, explaining the process as you go. [If you have a four-term polynomial to factor, you will need to use factoring by grouping. 

For the third problem, make sure you use the “ac method” to factor.

Answer 1

Factoring first expression

`w^(2) +8w +16`

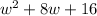
we can split
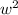`w^(2)` into two parentheses like this

(w )(w )------------------------------------------------(1)

Now to fill the blanks in each parentheses we make factors of constant term 16 and will pick those factors of 16 whose sum is middle term 8

So we can see pairs of factors of 16 as

(1,16); (2,8); (4,4).

out of these we can see that 4+4 gives 8. So +4 and +4 are pairs of factors of 16 that will work here.

So simply plug +4 in blank in first parentheses and +4 in blank in other parentheses in (1)

(w +4)(w +4)

so that the factored form.

We can also write this as
`(w+4)^(2)`

--------------------------------------------------------------------------------------------------------

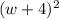
To factor
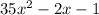`35x^(2) -2x -1` we will use AC method.

In this method we will first compare this expression with standard form

`ax^(2) +bx +c`

`35x^(2) -2x -1`

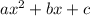
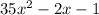
so a = 35, b = -2, c = -1

So ac = 35 × -1 = -35

So we will make factors of ac which is -35 here and will pick those factors of -35 which will give sum as b which is -2.

So pairs of factors of 35 are

(1,35); (5,7)

We can see that we can get sum as -2 form 5 and 7 if we take +5 and -7 as +5-7 =-2. So +5 and -7 factors will work here

So now split the middle term -2x in
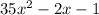`35x^(2) -2x -1` in factors +5 and -7. So we can rewrite -2x as +5x-7x

`35x^2 +5x -7x -1`

Now we will make two groups as shown

`(35x^2 +5x)+( -7x -1 )`

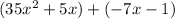
Now factor each group separately

in
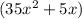`(35x^2 +5x)` we have greatest common factor as 5x so take that common out and divide all terms by 5x to get the terms left inside parentheses.

So we get 5x(7x+1) for this group

Similarly to factor (-7x-1) we can take greatest common factor -1 common out so we will have -1(7x+1)

5x(7x+1) -1(7x+1)

Now both terms have (7x+1) factor common so take that common out from both terms. So we will have

(7x+1)(5x-1)

So thats its factored form

---------------------------------------------------------------------------------------------------------

Again for third expression
`3y^(2) + 10y + 7`

we will use AC method to factor

So here a = 3, b = 10, c = 7

so ac = 3 × 7 = 21

So we will make factors of 21 and will pick those factors of 21 whose sum is b which is 10

Pair factors of 21 are

(1,21); (3,7)

We can see that factors 3+7 can give 10. So factors +3 and +7 will work here.

so split the middle term 10y in
`3y^(2) + 10y + 7` in terms of factors +3 and +7 so we can rewrite 10y as +3y+7y

`3y^(2) + 3y + 7y+ 7`

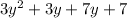
Now again make groups

`(3y^(2) + 3y ) + (7y+ 7)`

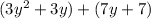
Factor each group separately by taking greatest common factor out in each group

3y(y+1) + 7(y+1)

As we can see both terms have factor (y+1) common in them so we can take (y+1) factor common out. So we will have final factored form as

(y+1)(3y+7)

------------------------------------------------------------------------------------------------------