Question

Coach Jamison wants to celebrate the final win of the school's baseball season with a trip to the local fast food place. The team buys 28 delicious tacos and 27 orders of savory nachos for $114.80. A few of the players are still hungry, so the coach buys 12 more tacos and 3 more orders of nachos for $37.20. If you don't consider tax, what is the price of a taco and the price of an order of nachos ?

Answer 1

So we have 2 variables here: tacos and orders of nachos.

When we translate the paragraphs into equation:
`28t + 27n = 114.80 \\ \\ 12t + 3n = 37.20`

Now, in this situation we can make use the elimination method by converting 3n to -27n.


`- 108t - 27n = - 334.8`

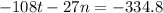
Add both equations:
`28t + 27n - 108t - 27n = 114.8 - 334.8 \\ \\ - 80t = - 220 \\ \\ t = 2.75`

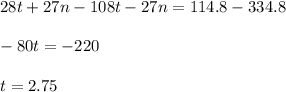
So we find that one taco costs $2.75.

We can plug this into any of the first two equations to find n:
`12 * 2.75 + 3n = 37.2 \\ \\ 33 + 3n = 37.2 \\ \\ 3n = 4.2 \\ \\ n = 1.4`

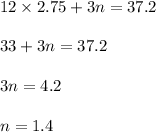
So one order of nachos cost $1.40.