Greetings!
To start this problem, let's first assign a variable for the missing, consecutive odd numbers. Since they are consecutive and odd, we add two.
Proof: 3-1=2, 5-3=2
The first, consecutive, odd number:

The second, consecutive, odd number:
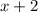
The third, consecutive, odd number:
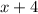
The fourth, consecutive, odd number:
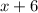
The sum of the values are equal to 3 times the sum of the first two numbers, of which this is equal to 35 less than the fourth number. Let's create an equation to simplify this:
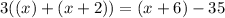
Complete the operations inside the parenthesis:
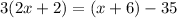
Distribute the parenthesis (utilizing the distributive property)
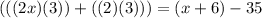
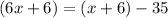
Simplify both sides:
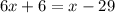
Add -6 and -x to both sides of the equation:


Divide both sides of the equation by 5:
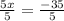
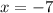
If
 is equal to -7:
is equal to -7:
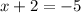
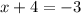

The four numbers are:
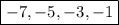
I hope this helps!
-Benjamin