Question

Find the equation of the tangent line to the curve y equals left parenthesis x minus 3 right parenthesis superscript 7 baseline left parenthesis x plus 1 right parenthesis squaredy=(x−3)7(x+1)2 at the point left parenthesis 4 comma 25 right parenthesis(4,25).

Answer 1

We have been given the expression to be
`y=(x-3)^7(x+1)^2`

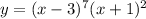
Since we need to find the tangent at a point, we will have to find the derivative of
`y` as the slope of the tangent at a given point on the curve is always equal to value of the derivative at that point.

Thus, we have to find
`(dy)/(dx)=(d)/(dx) (x-3)^7(x+1)^2`

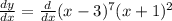
We will use the product rule of derivatives to find
`(dy)/(dx)`

Thus,
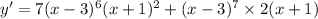`y'=7(x-3)^6(x+1)^2+(x-3)^7*2(x+1)` (using the product rule which states that
`(fg)'=f'g+fg'`)

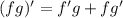Taking the common factors out we get:

`y'=(x-3)^6(x+1)(7(x+1)+2(x-3))`

`y'=(x-3)^6(x+1)(7x+7+2x-6)=(x-3)^6(x+1)(9x+1)`

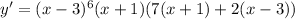
Thus,
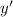`y'` at
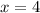`x=4` is given by:

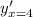`y'_(x=4)`=Slope of the tangent of y at x=4=
`m`

Thus,
`m=(4-3)^6(4+1)(9*4+1)=185`

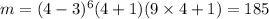
Now, the equation of the tangent line which passes through
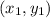`(x_(1), y_(1))` and has slope m is given by:

`y-y_(1)=m(x-x_(1))`

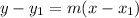
Thus, the equation of the tangent line which passes through
`(4,25)` and has the slope 185 is
`y-25=185(x-4)`

Which can be simplified to
`y=185x-740+25=185x-715`

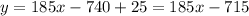
Thus,
`y=185x-715`

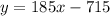
This is the required equation of the tangent.