Question

The half-life of nitrogen-13 is 10.0 minutes. if you begin with 53.3 mg of this isotope, what mass remains after 25.9 minutes have passed?

Answer 1

Hello!

The half-life is the time of half-disintegration, it is the time in which half of the atoms of an isotope disintegrate.

We have the following data:

mo (initial mass) = 53.3 mg

m (final mass after time T) = ? (in mg)

x (number of periods elapsed) = ?

P (Half-life) = 10.0 minutes

T (Elapsed time for sample reduction) = 25.9 minutes

Let's find the number of periods elapsed (x), let us see:

`T = x*P`

`25.9 = x*10.0`

`25.9 = 10.0\:x`

`10.0\:x = 25.9`

`x = (25.9)/(10.0)`

`\boxed{x = 2.59}`

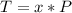
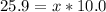
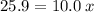
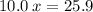
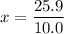
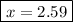
Now, let's find the final mass (m) of this isotope after the elapsed time, let's see:

`m = (m_o)/(2^x)`

`m = (53.3)/(2^(2.59))`

`m \approx (53.3)/(6.021)`

`\boxed{\boxed{m \approx 8.85\:mg}}\end{array}}\qquad\checkmark`

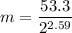
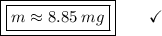
I Hope this helps, greetings ... DexteR! =)