Question

A statue is mounted on top of a 21 foot hill. From the base of the hill to where you are standing is 57feet and the statue subtends an angle of 7.1° to where you are standing. Find the height of the statue.

Answer 1

Please find the attached diagram for a better understanding of the question.

As we can see from the diagram,

RQ = 21 feet = height of the hill

PQ = 57 feet = Distance between you and the base of the hill

SR= h=height of the statue

`\angle SPR`=Angle subtended by the statue to where you are standing.

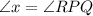`\angle x=\angle RPQ`= which is unknown.

Let us begin solving now. The first step is to find the angle
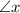`\angle x` which can be found by using the following trigonometric ratio in
`\Delta PQR` :

`tan(x)=(RQ)/(PQ) =(21)/(57)`

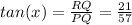
Which gives
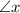`\angle x` to be:

`\angle x=tan^(-1)((21)/(57))\approx20.22^(0)`

Now, we know that
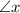`\angle x` and
`\angle SPR` can be added to give us the complete angle
`\angle SPQ` in the right triangle
`\Delta SPQ`.

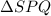We can again use the tan trigonometric ratio in
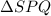`\Delta SPQ` to solve for the height of the statue, h.

This can be done as:

`tan(\angle SPQ)=(SQ)/(PQ)`

`tan(7.1^0+20.22^0)=(SR+RQ)/(PQ)`

`tan(27.32^0)=(h+21)/(57)`

`\therefore h+21=57tan(27.32^0)`

`h\approx8.45 ft`

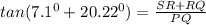
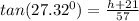
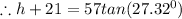
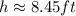
Thus, the height of the statue is approximately, 8.45 feet.