Given that, the variable z is directly proportional to x, and inversely proportional to y.
So, we can set up an equation as following:
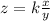 Where k = constant of variation.
Where k = constant of variation.
Another information given in the problem is, when x is 9 and y is 6, z has the value 19.5.
So, x = 9, y = 6 and z = 19.5.
Let's plug in these values in the above equation. So,
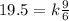
19.5 = k* 1.5
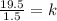 Divided each sides by 1.5 to isolate k.
Divided each sides by 1.5 to isolate k.
So, k = 13.
Hence, the equation will be
 .
.
Now we need to find the value of z when x= 14, and y= 11 . Therefore,
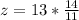
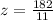
So, z= 16.5 (Rounded to tenth).
Hope this helps you!