To solve this question we will use two important formulas.
The first formula involves the calculation of the decay constant,
 which is to be found as:
which is to be found as:
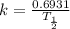
where
 is the half life of Pb-210 which is given to be 22 years in the question.
is the half life of Pb-210 which is given to be 22 years in the question.
Thus,
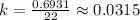
Now, we will use the second formula which is called the function of decay formula and is given as:
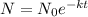
where
 percentage of Pb-210 remaining in the bone at present, which in our case is 67% or 0.67
percentage of Pb-210 remaining in the bone at present, which in our case is 67% or 0.67
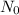 percentage of Pb-210 to start with, which is always 100% or 1.
percentage of Pb-210 to start with, which is always 100% or 1.
Plugging in all these values in the decay formula we are supposed to find the time,
 .
.

Taking natural log on both sides we get:
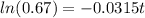
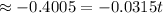
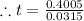
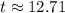 years
years
Therefore the bone fragment is about 12.71 years old.