Question

Last year, 150 cases were reported of a new infectious disease. It has been predicted that the number will double every year. How many cases will be reported in the ninth year?

Answer 1

This question is a simple application of the compounding formula.

The compounding formula is as:

`F=P(1+r)^n`

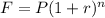
Here F is the future value

P is the present value

r is the rate at which the infection spreads in a year

n is the total number of years in consideration

Now, we know that the infection started spreading in the previous year and the question asks us How many cases will be reported in the ninth year from now. We will use the formula taking into the consideration that the total number of years is 10.

Thus, in the 9th year from now, the total cases of infection will be:

`F=150(1+1)^(10)=153600`

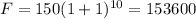
Thus, total reported cases in the 9th year will be 153600

Answer 2

38,400

Explanation:

This is a geometric sequence requiring that the 9th term be computed. The nth term of a geometric sequence is given as

Tn = ar^n-1

where Tn is the nth term, a is the first term, r is the common ratio of then sequence

r = T2/T1

where T2 and T1 are the second and first terms respectively

Given that last year, 150 cases were reported of a new infectious disease. It has been predicted that the number will double every year. It means that

a = 150, r = 2

therefore, the 9th term which is the value in the 9th year

= 150 * 2^9-1

= 150 * 256

= 38,400