Question

You yell into a canyon. You hear the echo in 3 seconds. How long did the sound of your voice travel before bouncing off a cliff?

Answer 1

The sound travelled 516 meters before bouncing off a cliff.

Step-by-step explanation:

The sound is an example of mechanical wave, which means that it needs a medium to propagate itself at constant speed. The time needed to hear the echo is equal to twice the height of the canyon divided by the velocity of sound. In addition, the speed of sound through the air at a temperature of 20 ºC is approximately 344 meters per second. Then, the height of the canyon can be derived from the following kinematic formula:

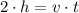`2\cdot h = v\cdot t` (1)

Where:

`h` - Height, measured in meters.

`v` - Velocity of sound, measured in meters per second.

`t` - Time, measured in seconds.

If we know that
`v = 344\,(m)/(s)` and
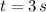`t = 3\,s`, then the height of the canyon is:

`h = (v\cdot t)/(2)`

`h = (\left(344\,(m)/(s) \right)\cdot (3\,s))/(2)`

`h = 516\,m`

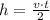
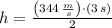
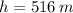
The sound travelled 516 meters before bouncing off a cliff.