Question

Find an equation of the plane passing through the point ​(1​,3​,2​) with a normal vector of the form nequalsleft angle a comma b comma 1 right angle that slices off the region in the first octant with the least volume.

Answer 1

P(1,3,2)

Normal vector <a, b, 1>

Without much fuss we can write the plane with that normal through our point. The normal components become the coefficients and x, y and z and we plug in the point to get the constant:

ax + by + 1 z = a(1) + b(3) + 1(2)

ax + by + z = a + 3b + 2

Let's call the x y and z intercepts (p,0,0), (0,q,0) and (0,0,r)

Then the volume of our octant slice is the volumne of a right pyramid with base right triangle legs p and q and height r, so, if I remember everything correctly,

`V = \frac 1 3 (\frac 1 2 p q) r = \frac 1 6 p q r`

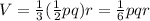
Now we have to calculate the intercepts, gotten by setting the other two variables to zero.

ax + by + z = a + 3b + 2

ap + b(0) + (0) = a + 3b + 2

p = (a+3b+2)/a

q = (a+3b+2)/b

r = a + 3b + 2

`6V = pqr=( (a+3b+2)^3)/(ab)`

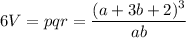
We need to minimize the two partials; we can basically ignore the factor of 6.

`0= (\partial 6V)/(\partial a) = ( ab ( 3(a+3b+2)^2)(1) - (a+3b+2)^3(b) )/(a^2b^2) = ( ( 3a - (a+3b+2)) (a+3b+2)^2)/(a^2b) = ( ( 2a -3b-2) (a+3b+2)^2)/(a^2b)`

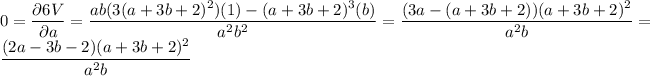
2a -3b-2 = 0 or a+3b+2 = 0

`0= (\partial 6V)/(\partial b) = ( ab ( 3(a+3b+2)^2)(3) - (a+3b+2)^3(a) )/(a^2b^2) = ( ( 9b - (a+3b+2)) (a+3b+2)^2)/(ab^2) = ( ( 6b-a-2) (a+3b+2)^2)/(ab^2)`

6b-a-2 = 0 or a+3b+2 = 0

2a -3b= 2

-a + 6b = 2

-2a + 12b = 4

Adding,

9b = 6

b = 2/3

a = 6b - 2 = 2

2x + (2/3)y + z = 6

Answer: 2x + (2/3)y + z = 6

I'd have to meditate on the check but it's 4am here so goodnight.