Answer:
The sum of 8 term of the series is
 or 127.5
or 127.5
Explanation:
Given: The series
 + 1 +2 +4 + ...
+ 1 +2 +4 + ...
We need to find the sum of 8 term
Common ratio, r
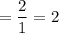
First term,
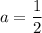
n=8
Formula:
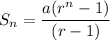
Substitute the value of a, r and n into formula
Sum of 8th term of the sequence
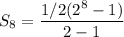
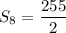
Hence, The sum of 8 term of the series is
 or 127.5
or 127.5