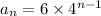Question

In the 1st generation, there are 6 squirrels in a forest. Every generation after that, the squirrel population multiplies by 4. In generation 2 there are 24 squirrels, in generation 3 there are 96 squirrels, and so on. Which explicit formula can be used to find the number of squirrels in the nth generation?

Answer 1

Option B is correct.i.e., No of squirrels in nth generation
`a_n=6*4^(n-1)`

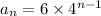
Explanation:

Given:

No of squirrels in 1st Generation = 6

No of squirrels in 2nd generation = 24

No of squirrels in 3rd generation = 96

Option A).

No of squirrels in nth generation
`a_n=4*6^(n-1)`

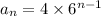
From formula,

No of squirrels in 1st generation
`a_1=4*6^(1-1)=4`

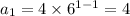
So, This option is wrong.

Option B).

No of squirrels in nth generation
`a_n=6*4^(n-1)`

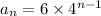
From formula,

No of squirrels in 1st generation
`a_1=6*4^(1-1)=6`

No of squirrels in 2nd generation
`a_2=6*4^(2-1)=6*4=24`

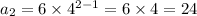
No of squirrels in 3rd generation
`a_3=6*4^(3-1)=6*16=96`

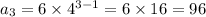
So, This option is correct.

Therefore, Option B is correct.i.e., No of squirrels in nth generation
`a_n=6*4^(n-1)`

Answer 2

The appropriate choice is

... B. an = 6·4^(n-1)

The general term of a geometric sequence with first term a1 and common ratio r is given by

... an = a1·r^(n-1)

Your sequence has a1=6 and r=4. The answer above is the result of substituting the given numbers for the corresponding variables in the general formula.