Question

Prove cotx=sinxsin(\frac{\pi}{2}-x)+cos^{2}xcotx [/tex]

Answer 1

We have to prove that :

`Cot(x)=Sin(x)Sin((\pi)/(2)-x)+Cos^(2)(x)Cot(x)`

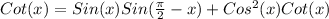
For this, let us take the Right Hand Side (RHS) and then prove the Left Hand Side (LHS).

RHS=
`Sin(x)Sin((\pi)/(2)-x)+Cos^(2)(x)Cot(x)`

=
`Sin(x)Cos(x)+Cos^(2)(x)Cot(x)` (
`\because Sin((\pi)/(2)-x)=Cos(x)`)

=
`Sin(x)Cos(x)+Cos^(2)(x)(Cos(x))/(Sin(x))` (
`\because Cot(x)=(Cos(x))/(Sin(x))`)

=
`(Sin^2(x)Cos(x)+Cos^2(x)Cos(x))/(Sin(x))`

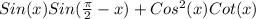
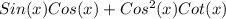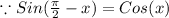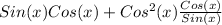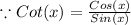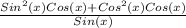
Now, we know that
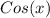`Cos(x)` is common in the numerator and thus,

`(Cos(x)(Sin^2(x)+Cos^2(x)))/(Sin(x))`

=
`(Cos(x))/(Sin(x))` (
`\because Sin^2(x)+Cos^2(x)=1`)

=
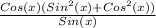
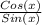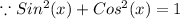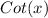`Cot(x)`=LHS

Hence, LHS=RHS and thus the required equation has been proved.