Question

What is the value of

Answer 1

`\left( \frac 2 3 \right)^(-4) = \left( \frac 3 2 \right)^4 = (3^4)/(2^4) = (81)/(16)`

Second choice

Answer 2

For this case we have the following expression:

`((2)/(3))^(-4)`

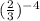
By properties of powers we can rewrite the given expression.

We have then:

`(1)/(((2)/(3))^4)`

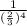
Then, rewriting the denominator of the fraction we have:

`(1)/((16)/(81))`

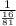
Finally rewriting the fraction we have:

`(81)/(16)`

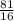
Answer:

The equivalent expression is given by:

`(81)/(16)`

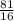
option 1