Question

A 350-foot water slide has a 32-foot vertical drop. What is the angle of depression?

Answer 1

Please find the attached diagram for a better understanding of the solution given here.

B is the base of the Vertical Drop. Thus, AB=32 feet.

AC is the water slide and thus the length of AC is 350 feet.

We need to find the angle of depression which in this case is
`\angle X`.

As can be seen from the diagram,
`\angle Y` and
`\angle X` are alternate interior angles where the water slide, AC, is the transversal and thus they will be equal.

therefore,
`\angle X = \angle Y`

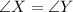
Let us make use of the
`\Delta ABC` to find
`\angle Y` using the Sine trigonometric ratio.

Thus,
`Sin (\angle Y)=(Opposite Side)/(Hypotenuse) =(AB)/(AC)`

`\therefore Sin(\angle Y)=(32)/(350)`

`\angle Y=Sin^(-1)((32)/(350))=\approx5.246^0`

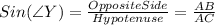
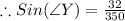
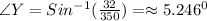
Thus Angle of Depression is
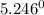`5.246^0`, which the required answer.