Answer:
Mark's monthly payment is $1386.40.
Explanation:
Marc bought a new split level for $200,000. Marc put down 30%.
So, loan amount =
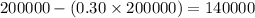 dollars
dollars
p = 140000
r =
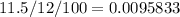
n = 360
The EMI formula is :
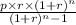
Substituting the values in the formula:

=>
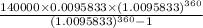
= $1386.40
Hence, Mark's monthly payment is $1386.40.