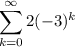Each term seems like it's -3 times the previous one, first term 2.
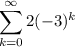
Going to infinity like that it's of course divergent, but perfectly summable if we replace infinity with a finite bound like n-1:
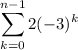
But, assuming the pattern continues means I'd go with infinity.
Answer: