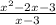Question

Shawn found that a solution of x = 3 was extraneous for his function. What would be a possible denominator in Shawn's function?

2x + 6
x2 − 2x − 3
x2 + 6x + 9
4x − 11

Answer 1

Your answer is B. x2 -2x -3

Hope this helps!!

Answer 2

Option B is correct

Explanation:

Given: A solution x =3 was extraneous for his function.

Extraneous solution defined as a root of a transformed equation that is not a root of the original equation because it was excluded from the domain of the original equation.

The only function from the given options

f(x) =
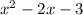`x^2-2x-3` has the solution x =3

therefore,

3 is excluded from the domain of the
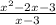`(x^2-2x-3)/(x-3)` because it would make the denominator of one of the fractions zero and division by zero is not allowed.

Therefore, it cannot be a root of the equation
`(x^2-2x-3)/(x-3)`