Answer:
The ordered pair (-3, 12) DOES NOT satisfy the equation.
Explanation:
Given the function
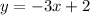
Let us substitute all the values to check which points satisfy the function.
FOR (1, -1)
y = -3x+2
substitute x = 1, y = -1
-1 = -3(1) + 2
-1 = -3+2
-1 = -1
TRUE!
Thus, the ordered pair (1, -1) satisfies the equation.
FOR (4, -10)
y = -3x+2
substitute x = 4, y = -10
-10 = -3(4) + 2
-10 = -12+2
-10 = -10
TRUE!
Thus, the ordered pair (4, -10) satisfies the equation.
FOR (-2, 8)
y = -3x+2
substitute x = -2, y = 8
8 = -3(-2) + 2
8 = 6 + 2
8 = 8
TRUE!
Thus, the ordered pair (-2, 8) satisfies the equation.
FOR (-3, 12)
y = -3x+2
substitute x = -3, y = 12
12 = -3(-3) + 2
12 = 9+2
12 = 11
L.H.S ≠ R.H.S
FALSE!
Thus, the ordered pair (-3, 12) DOES NOT satisfy the equation.
Therefore, the ordered pair (-3, 12) DOES NOT satisfy the equation.