Question

Use the equation and type the ordered-pairs.

y = log2 x
{(1/2,?), (1, ?), (2, ?), (4,?), (8,?), (16, ?)}

Answer 1

Given the equation

y=
`\[log_2(x)\]`

{(1/2,?), (1, ?), (2, ?), (4,?), (8,?), (16, ?)}

Lets start with (1/2, ?)

Ordered pair is (x,y)

In (1/2, ?) , x=1/2 and we need to find out y

y=
`\[log_2(x)\]`

Plug in 1/2 for x, y=
`\[log_2(1/2)\]` =
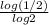`(log(1/2))/(log2)` = -1

we do the same for all ordered pairs

(1, ?)

Plug in 1 for x, y=
`\[log_2(1)\]` =
`(log(1))/(log2)` = 0

(2, ?)

Plug in 2 for x, y=
`\[log_2(2)\]` =
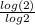`(log(2))/(log2)` = 1

(4, ?)

Plug in 4 for x, y=
`\[log_2(1)\]` =
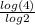`(log(4))/(log2)` = 2

(8, ?)

Plug in 8 for x, y=
`\[log_2(8)\]` =
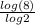`(log(8))/(log2)` = 3

(16, ?)

Plug in 16 for x, y=
`\[log_2(16)\]` =
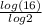`(log(16))/(log2)` = 4

Ordered pairs are

{(1/2,-1), (1, 0), (2, 1), (4,2), (8,3), (16, 4)}