Question

Assume that a sample is used to estimate a population proportion p. find the margin of error e that corresponds to the given statistics and confidence level. round the margin of error to four decimal places. ​99% confidence; the sample size is 1 comma 1801,180​, of which 3030​% are successes

Answer 1

Let p be the proportion. Let c be the given confidence level , n be the sample size.

Given: p=0.3, n=1180, c=0.99

The formula to find the Margin of error is

ME =
`z _(\alpha/2) \sqrt{(p*(1-p))/(n)}`

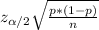
Where z (α/2) is critical value of z.

P(Z < z) = α/2

where α/2 = (1- 0.99) /2 = 0.005

P(Z < z) = 0.005

So in z score table look for probability exactly or close to 0.005 . There is no exact 0.005 probability value in z score table. However there two close values 0.0051 and 0.0049 . It means our required 0.005 value lies between these two probability values.

The z score corresponding to 0.0051 is -2.57 and 0.0049 is -2.58. So the required z score will be average of -2.57 and -2.58

(-2.57) + (-2.58) = -5.15

-5.15/2 = -2.575

For computing margin of error consider positive z score value which is 2.575

The margin of error will be

ME =
`z _(\alpha/2) \sqrt{(p*(1-p))/(n)}`

=
`2.575 \sqrt{(0.30*(1-0.3))/(1180)}`

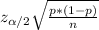
= 2.575 * 0.0133

ME = 0.0342

The margin of error is 0.0342