Answer:
Option 2 is right
(1/2,1)
Explanation:
Given is a function with graph as
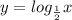
Here 1/2 is the base
We find that when x=1, log x =0 and hence (1,1/2) does not lie on this graph
(1/2,1)
When x =1/2, f(x) = log of a number to its own base =1
Thus (1/2,1) satisfies this equation and hence lies on the graph
(0,1) is not right because log x is not defined and not finite.
So only option 2 is right