Question

Please help me with this!

Answer 1

Volume of the cube = a³ (Given)

`\boxed{ \text{Volume of a cube = side}^3}`

Side of a cube = ∛a³ = a

Side of the cube after it increased by b = a + b

`\boxed{\text{Area of a cube = side}^2}`

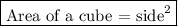
Area of the cube = (a + b)²

Increase in area = (a + b)² - a²

-

Simplify (a + b)² - a²:

(a + b)² - a²

Open (a + b)² as a² + 2ab + b² :

= a² + 2ab + b² - a²

Combine a² and -a²:

= 2ab + b²

Take out b as the common factor:

= b(2a + b)

-

Answer: (H) b(2a + b)

Answer 2

The original area of a face would be a^2. Now that you added b to the edge, the new area of each face would be (a+b)^2. To find how much the are increased, subtract a^2 from (a+b)^2.
`(a+b)^2-(a^2)= a^2+2ab+b^2-(a^2)= 2ab+b^2= b(2a+b)` So the answer is b(2a+b)