Question

What is the solution set for 2x+5y>-1 and 4x-3<-3?

Answer 1

PROBLEM ONE

•

Solving for x in 2x + 5y > -1.

•

Step 1 ) Subtract 5y from both sides.

2x + 5y > -1

2x + 5y - 5y > -1 - 5y

2x > -1 - 5y

Step 2 ) Divide both sides by 2.

2x > -1 - 5y

`\displaystyle(2x)/(2) > \displaystyle(-1 - 5y)/(2)`

`\displaystyle\ x > (-1 - 5y)/(2)`

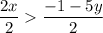
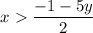
So, the solution for x in 2x + 5y > -1 is...

`\displaystyle\ x > (-1 - 5y)/(2)`

•

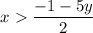
Solving for y in 2x + 5y > -1.

•

Step 1 ) Subtract 2x from both sides.

2x + 5y > -1

2x - 2x + 5y > -1 - 2x

5y > -1 - 1x

Step 2 ) Divide both sides by 5.

5y > -1 - 1x

`\displaystyle(5x)/(5) > (-1 -1x)/(5)`

`\displaystyle\ x > (-1 -1x)/(5)`

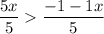
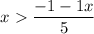
So, the solution for y in 2x + 5y > -1 is...

`\displaystyle\ x > (-1 -1x)/(5)`

•

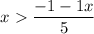
PROBLEM TWO

•

Solving for x in 4x - 3 < -3.

•

Step 1 ) Subtract 3 from both sides.

4x - 3 < -3

4x -3 - 3 < -3 - 3

4x < 0

Step 2 ) Divide both sides by x.

4x < 0

`\displaystyle(4x)/(4) <(0)/(4)`

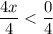
x < 0

So, the solution for x in 4x - 3 < -3 is...

x < 0

•

•

- Marlon Nunez