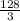2 Answers

Steve Koch · Answer 1 · 2019-12-12T03:20:49+0000

By definition, the volume of the cylinder is given by:

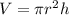
$V= \pi r^2h$

On the other hand, we know that the height of the sphere is:

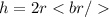
The height of the sphere is equal to the height of the cylinder, therefore, rewriting the volume of the cylinder we have:

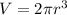
$V= 2 \pi r^3$

Substituting the cylinder volume value we have:

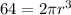
$64= 2 \pi r^3$

Then, by definition, the volume of the sphere is given by:

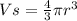
$Vs = (4)/(3) \pi r^3$

Rewriting we have:

$Vs = (2)/(3) 2 \pi r^3$

Substituting values we have:

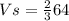
Vs = (2)/(3) 64

Rewriting we have:

(128)/(3)

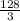
Answer:

The volume of the sphere is given by:

(128)/(3)

Please log in or register to add a comment.