we need to find the probability that if an individual passenger is randomly selected, their weight will be greater than 166 lb.
Assume that weights of passengers are normally distributed with a mean of 177 lb and a standard deviation of 41.4 lb.
Mean = 177
standard deviation = 41.4
We find z-score using given mean and standard deviation
z =
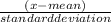
=
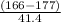 = -0.265700
= -0.265700
Probability (z>-0.26570) = 1 - 0.3974 (use normal distribution table)
= 0.6026
P(weight will be greater than 166 lb) = 0.6026