Question

Select the correct answer from each drop-down menu. Consider this system of equations: -3x + 5y = 22 (equation 1) 20y − 11 = 12x (equation 2) This system of linear equations represents a. coincidental b. Intersecting c. parallel lines. The system of equation 1 and the equation 20y = 12x + 88 represents a. coincidental b. Intersecting c. parallel lines.

Answer 1

(1st):

-3x + 5y = 22

5y = 3x + 22

y = 3/5 x + 22/5; slope = 3/5

(2nd):

20y − 11 = 12x

20y = 12x + 11

y = 12/20 x + 11/20

y = 3/5 x + 11/20; slope = 3/5

Both lines have same slope so both lines are parallel.

Answer: c. parallel lines.

--------------------

The system of equation 1: -3x + 5y = 22 has slope = 3/5

20y = 12x + 88

20y = 12x + 88

y = 12/20 x + 88/20

y = 3/5 x + 22/5. slope = 3/5

Both have same slope

Answer

c. parallel lines.

Answer 2

Answer with Step-by-step explanation:

If two lines on the same plane have different slopes, they are intersecting lines.

If two equations can be transformed to one form and they are equal, they are coinciding lines.

for parallel lines their slope (m) must be equal and their y-intercept (b) must be different.(y=mx+b)

-3x + 5y = 22 (equation 1) or 5y=22+3x

or
`y=(3)/(5)x+(22)/(5)`

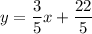
20y − 11 = 12x (equation 2)

or 20y=12x+11

`y=(12)/(20)x+(11)/(20)\\\\or\ y=(3)/(5)x+(11)/(20)`

Hence, we can see clearly the two lines have same slope 3/5 but y intercept is different

So, two lines are parallel

Hence, Correct option is:

c. parallel lines