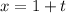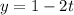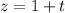Question

g Find the equation of the line passing through the point (1, 1, 1) which is perpendicular to the plane containing the points (1, 0, 0), (2, 1, 1) and (1, 1, 2).

Answer 1

The equation of the line is given by:

`x = 1 + t`

`y = 1 - 2t`

`z = 1 + t`

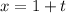
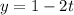
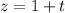
Explanation:

Parametrizing the equation of the line in function of t, the equation of the line is given by:

`x = x_0 + at`

`y = y_0 + bt`

`z = z_0 + ct`

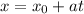
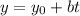
In which we have an initial point
`(x_0,y_0,z_0)` and
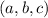`(a,b,c)` is a vector parallel to the line.

Line passing through the point (1, 1, 1)

This means that
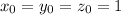`x_0 = y_0 = z_0 = 1`. So

`x = 1 + at`

`y = 1 + bt`

`z = 1 + ct`

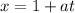
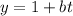
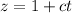
Perpendicular to the plane containing the points (1, 0, 0), (2, 1, 1) and (1, 1, 2).

From this, we get two vectors:

`(2-1,1-0,1-0) = (1,1,1)`

`(1-2,1-1,2-1) = (-1,0,1)`

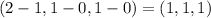
The parallel vector is given by the determinant of the following matrix:

`\left[\begin{array}{ccc}i&j&k\\1&1&1\\-1&0&1\end{array}\right]`

Which is:

`D = i*1*1 + j*1*-1 + k*1*0 - k*1*(-1) - j*1*1 -i*1*0`

`D = i - j + k - j`

`D = i - 2j + k`

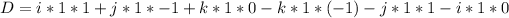
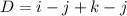
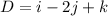
So the vector is (1,-2,1), and the equation of the line is:

`x = 1 + t`

`y = 1 - 2t`

`z = 1 + t`