Question

Which is the equation in standard form of the line that contains points C and D?

Answer 1

Hello!

The standard form a linear equation is Ax + By = C, where A, B, and C are real numbers, and A is a positive integer.

To find the standard form of these two points, we can find the slope-intercept form of the equation, and then convert it into standard form.

Slope-intercept form is written as: y = mx + b. In this formula m is the slope, and b is the y-intercept.

First, we can find the slope by using the slope formula:
`(y_(2)-y_(1))/(x_(2)-x_(1))`.

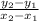Given the two points, C, which is (-2, -4), and D, which is (2, 2), we can substitute these values into the slope formula.

`(2 - (-4))/(2 - (-2)) = (6)/(4) = (3)/(2)`.

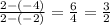The slope is 3/2. Next, we find the y-intercept. To find it, we need to substitute a point into this equation, and find b: y = 3/2x + b. We'll use the ordered pair, (2, 2).

2 = 3/2(2) + b

2 = 3 + b (subtract 3 from both sides)

b = -1

The equation that goes through the points C and D in slope-intercept form is y = 3/2x - 1.

Now, we need to change this equation into standard form.

y = 3/2x - 1 (multiply everything by 2)

2y = 3x - 2 (subtract -3x from both sides)

2y - 3x = -2

Since the standard and the slope-intercept form of the equation is not given, we can find the point-slope form of the two points.

Point-Slope Form: y -
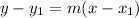`y - y_(1) = m(x - x_(1))`, and in this equation m is the slope, and y sub 1 and x sub 1 is one ordered pair. There are be two equations, since we were given two points.

y - 2 = 3/2(x - 2) OR y + 4 = 3/2(x + 2).

Therefore, the equation of the line that contains points C and D is choice C, with the equation, y - 2 = 3/2(x - 2).