Answer:
1)
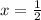
2)

Explanation:
We are asked to find value of x for each of our given expressions.
1).
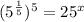
Substitute
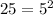 :
:
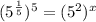
Using exponent property
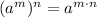 , we will get:
, we will get:

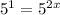
We know when
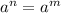 , then
, then
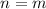 . Since base of both exponents is equal, so we can equate them as:
. Since base of both exponents is equal, so we can equate them as:
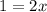
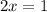
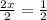
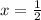
Therefore, the value of x is
 .
.
(2).

Using exponent property
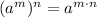 , we will get:
, we will get:
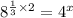
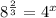
Substitute
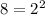 and 4 as Substitute
and 4 as Substitute
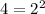 :
:
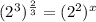
Using exponent property
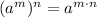 , we will get:
, we will get:
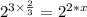
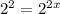
We know when
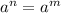 , then
, then
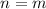 . Since base of both exponents is equal, so we can equate them as:
. Since base of both exponents is equal, so we can equate them as:
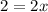
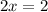
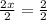

Therefore, the value of x is 1.