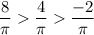Answer:
The function that has the greatest rate of change is:
g(x)
Explanation:
We know that the rate of change from x=a to x=b is determined as:
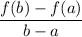
We are asked to find the rate of change of each of the functions form x=0 to x=pi over 2.
f(x):
We are given that:
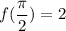
and,
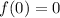
Hence,
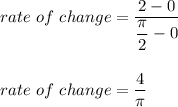
g(x):
We have:
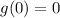
and

Hence,
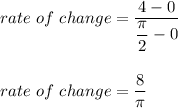
h(x):
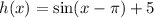
Now we have:
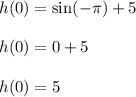
Also,
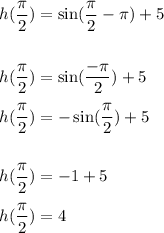
Hence, the rate of change is calculated as:
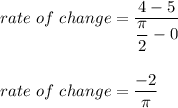
Hence, the greatest rate of change is:
g(x)
Since,