We have to decide if the square root is the radical sign, meaning the principal square root, or a multivalued square root.
Let's assume this is the radical sign applied to the radicands, indicating both sides are the principal square root.
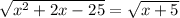
In this case, dealing with the principal values, it's ok to square both sides. Both sides are positive (or a positive number times i); we won't introduce extraneous roots.
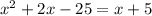
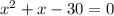
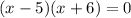
Answer: x=5 or x=-6
Check:
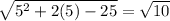
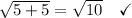
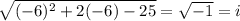
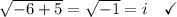
I suppose it depends what grade you're in as to whether you'll accept x=6 as a solution.
Answer (restricting ourselves to real square roots): x=5