Question

The birth weights for twins are normally distributed with a mean of 2353 grams and a standard deviation of 647 grams. use​ z-scores to determine which birth weight could be considered unusual.

a. 1200 g
b. 2353 g
c. 2000 g
d. 3647 g

Answer 1

Let X be the birth weight for twins which is normally distributed with mean μ = 2353 and standard deviation σ =647

Any z score value below -2 and above 2 is considered to e unusual. If the z score values lies between -2 and 2 then it is said to usual.

To find unusual birth weight first we will find z score for each x value. The x value with z score less than -2 or greater than 2 is said to be unusual.

a. x=1200

z =
`(x-mena)/(standard deviation)`

z =
`(1200-2353)/(647)`

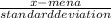
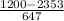
z = -1.78

Here z score is between -2 and 2 hence x=1200 is usual.

b. 2353

z =
`(2353-2353)/(647)`

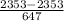
z = 0

Here z=0 lies between -2 and 2 hence x=2353 is usual.

c. 2000

z =
`(2000-2353)/(647)`

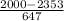
z = -0.5456

The z score -0.5456 lies between -2 and 2, hence x=2000 is usual.

d. 3647

z =
`(3647-2353)/(647)`

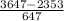
z = 2

The z score value 2 is upper bound for unusual z score value range. Hence x=3647 is usual.