Answer:
1. Mass percent of ethanol = 28.02 %.
2. Mole fraction of ethanol = 0.13.
Step-by-step explanation:
1. To find the mass percent we need to use the following equation:
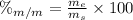
Where:
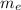 is the mass of ethanol
is the mass of ethanol
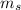 is the mass of the solution
is the mass of the solution
We need to calculate the mass of ethanol and the mass of the solution:

Where:
d: is the density of the solution = 0.957 g/mL
V: is the volume = 1 L
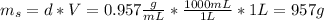
Now, from the concentration we can find the mass of ethanol:
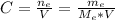
Where:
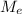 : is the molar mass of ethanol = 46.07 g/mol
: is the molar mass of ethanol = 46.07 g/mol
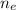 : is the number of moles of ethanol = m/M
: is the number of moles of ethanol = m/M

Finally, the mass percent of ethanol is:
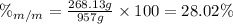
2. The mole fraction of ethanol is given by:
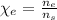
The number of moles of ethanol is:

And the moles of the solution is:

Where w is for water

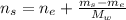
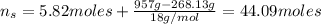
Hence, the mole fraction of ethanol is:
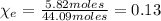
I hope it helps you!