Question

Assume that the weight loss for the first month of a diet program varies between 6 pounds and 12​ pounds, and is spread evenly over the range of​ possibilities, so that there is a uniform distribution. find the probability of the given range of pounds lost. less than 99 pounds

Answer 1

If the distribution is uniform between 6 and 12, the probability of being less than 99 is 1 (certainty).

_____

Perhaps you intend to find the probability that the loss is less than 9 pounds. That value is

... (9 - 6)/(12 - 6) = 3/6 = 1/2

Answer 2

Answer: 0.5

Explanation:

The probability density function for x that uniformly distributed in interval [a,b] :

`f(x)=(1)/(b-a)`

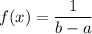
We assume that the weight loss for the first month of a diet program varies between 6 pounds and 12​ pounds and is spread evenly over the range of​ possibilities, so that there is a uniform distribution.

Let x be the weight loss for the first month of a diet program.

Density function =
`f(x)=(1)/(12-6)=(1)/(6)`

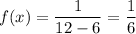
Now , the probability of the given range of pounds lost is less than 9 pounds :

`=\int^(12)_(9)\ f(x)\ dx\\\\= \int^(12)_(9)\ (1)/(6)\ dx\\\\= (1)/(6)[x]^(12)_(9)\\\\=(1)/(6)(12-9)=0.5`

Hence, the required probability = 0.5