Question

Martin can reasonably guess that the standard deviation for the entire population of people at the mall during the time of the survey is $1.50. What is the 95% confidence interval about the sample mean? Interpret what this means in the context of the situation where 95 people were surveyed and the sample mean is $8. Use the information in this resource to help construct the confidence interval.

Answer 1

We are given the following data in the above statement:

Sample mean = u = 8

Population standard deviation = x = 1.50

Sample size = n = 95

Confidence Interval = 95%

Since we know the population standard deviation we can use z distribution to find the confidence interval. The z value for the 95% confidence interval is:

z = 1.96

The formula for the confidence interval about the mean is:

`(u - z(s)/(√(n)) , u + z(s)/(√(n)))`

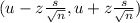
Using the values, we get the confidence interval:

`(8-1.96(1.5)/(√(95)) , 8-1.96(1.5)/(√(95)) )\\ \\ (7.70,8.30)`

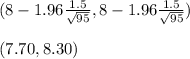
We are 95% confident that the true value of the population mean is in between 7.70 and 8.30 .