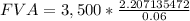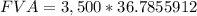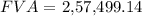Answer : The calculated answer of FVA is $ 2,57,499.14. This is closest to $257,502.00 - option B.
We follow these steps to arrive at the answer:
We use the Future Value of Annuity formula to arrive at the answer to this question, as the new account begins at $0.00 and there is no mention of the amount in the previous account.
The formula for Future Value of annuity is:

where
P = constant periodic contribution
r = rate per period
n = number of periods.
In the question above, P = $7,000.
The given interest rate is 12% p.a. Since the contributions are made semi-annually (twice a year), we need to find the rate per period with the following formula:
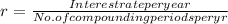
So, we get
r =
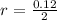
r = 0.06
Since there are two compounding periods per year, we get number of compounding periods 'n', by
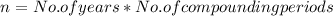
So,
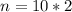
n = 20
Substituting the values of P, n and r in the FVA equation we get,