Question

For a particular rectangle, three times the width is 23 meters longer than the length. The area of the rectangle is 400 square meters. What is the perimeter of the rectangle?

Answer 1

Concept:

(i) In general, the length of any rectangle is always greater than its width.

(ii) Area of rectangle (A) = L × B

(iii) Perimeter of rectangle (P) = 2 ( L + B)

Given: Area of rectangle 'A' = 400 square meters

Let 'L' and 'B' be the length and width of the given rectangle.

According to the problem,

L = 3 B - 23 ------------------(1)

Area of the rectangle = 400 m²

or, L× B = 400 m²

or, (3 B - 23 )×B = 400

or, 3 B² - 23 B - 400 = 0

Apply, discriminant method,

Here, we will calculate only the positive value of B because width or length will never be negative.

`B = \frac{23 +\sqrt{23^(2)+(4)(3)(400)}}{2(3)}\\ B = 16`

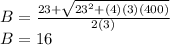
Now, using equation (1),

L = 3 B -23 = 3×16 - 23 = 25 m

Hence, length (L) = 25 m and Width (B) = 16 m

Now, we shall calculate the perimeter (P) of the rectangle

P = 2( L + B)

or, P = 2 (25 + 16 ) m

or, P = 82 m

Hence, the required perimeter of the given rectangle will be 82 m