Question

A manufacturer claims that fewer than 6% of its fax machines are defective. to test this claim, he selects a random sample of 97 such fax machines and finds that 5% are defective. find the p-value for the test of the manufacturer's claim. 0.1591

Answer 1

Let P be the population proportion, p be the sample proportion, n be the sample size.

A manufacturer claims that fewer than 6% of its fax machines are defective. It means P=0.06

Sample size n=97 and sample proportion p=0.05

The hypothesis to be tested is

H0: P ≥ 0.06 V/s Ha: P < 0.06

Here the hypothesis for testing population proportion we use z test statistics. Z test statistics is give by

Z =
`\frac{p -p_(0)}{\sqrt{p_(0)(1-p_(0))/n}}`

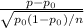
Where p =sample proportion = 0.05

p0 = hypothesized proportion value =0.06

Using given values into test statistics we get

Z =
`(0.05 -0.06)/(√(0.06(1-0.06)/97))`

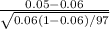
Z = -0.41

The p-value for left tailed alternative hypothesis is given by

P-value = P(z < z cal)

where zcal = Z test statistics value

Here zcal = -0.41

P-value = P(Z < -0.41)

Using z score table to find probability below z=-0.41

P-value = 0.3409

P-value for testing the given claim is 0.3409